Measuring the reliability of the consensus prediction
Measuring the reliability of the consensus prediction
The source code of the HMMTOP program has been modified in order to calculate the sum of the posterior probabilities along the Viterbi path. According to the unique hidden structure of the HMMTOP, the posterior probabilities were summed up for each main hidden state type (inside,membrane, loop and outside) in each position of the amino acid sequence, then these probabilities were summed up along the most probable state sequence provided by the Viterbi algorithm. We use this sum divided by the length of the protein to measure the reliability.
Assuming the notations of Rabiner’s excellent tutorial on hidden Markov models, the posterior probabilities can be calculated from the forward and backward variables:
where n is the sequence length, N is the number of states in the hidden Markov model, O is the array of observation symbols (the amino acid sequence) and λ is the hidden Markov model. The posterior probability of each main state can be calculated by summing up the posterior probabilities, which have the same label as the main state:
Reliability is the average of the posterior probabilities along the most probably state path (q):
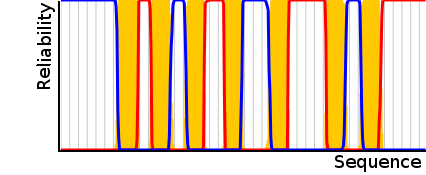A diagram on the right shows a certain prediction. In this case the
sum of the reliability through
the Viterbi path is 97% (red: inside,
blue: outside, yellow: trans-membrane).
The reliability highly correlates with the prediction accuracy, measured on the benchmark set, therefore it can be used to estimate the prediction accuracy of an individual prediction without any information about the topology at all.